Questions
Create quality questions from a wide variety of input options
Questions
Questions are the fundamental unit of content in PrairieLearn. While questions can be completely static, the key feature of PrairieLearn questions is the ability to generate, display, and grade many unique variants of the same base question.
Write it once, use many times!
Since questions are defined as code, they can be reused in many future assessments. And students can keep trying new variants of difficult problems until they've mastered the topic—no need for you to manually write new questions to give students extra practice.
Question templates
Check out these template questions - they can be great resources when creating your own questions.
Multiple-choice and checkbox answers


Text answers
Correct answer and distractors are randomly selected from a list of several correct answers and distractors.
Images answers
Correct answer and distractors are randomly selected from a list of images.
Randomized prompt
Correct answer and distractors are randomly selected from a list which is dynamically generated based on the choice of randomized prompt.
True/False answers
Randomly selects the prompt from a list and its corresponding True / False answer. Ensures the True option always appears first.
Multiple select answers
Randomly selects the question prompt and its corresponding correct/incorrect answers from a list.Numerical Answers

Randomized parameters
Computes the numerical answer using fixed mathematical expression given randomized input parameters.
Randomized prompt
Computes the numerical answer using a mathematical expression randomly selected from a list of options, given randomized input parameters.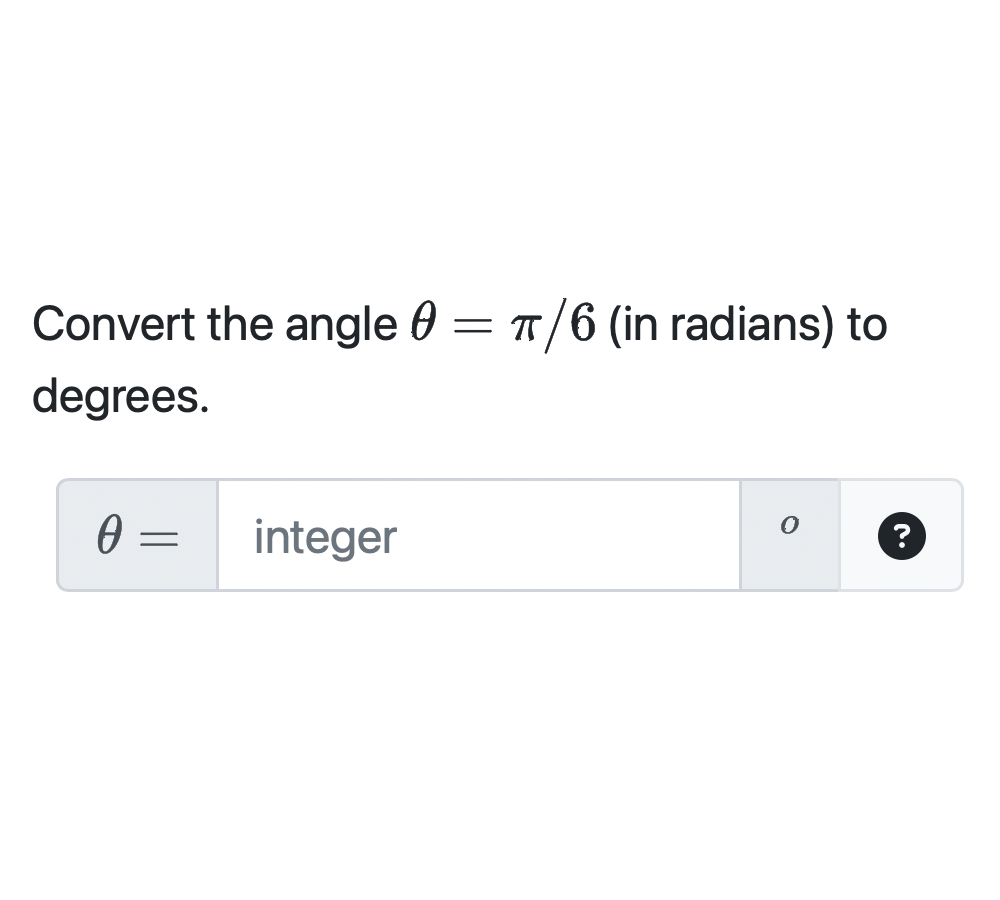
Integer answer
Computes the answer, expected to be an integer, given a randomized parameter.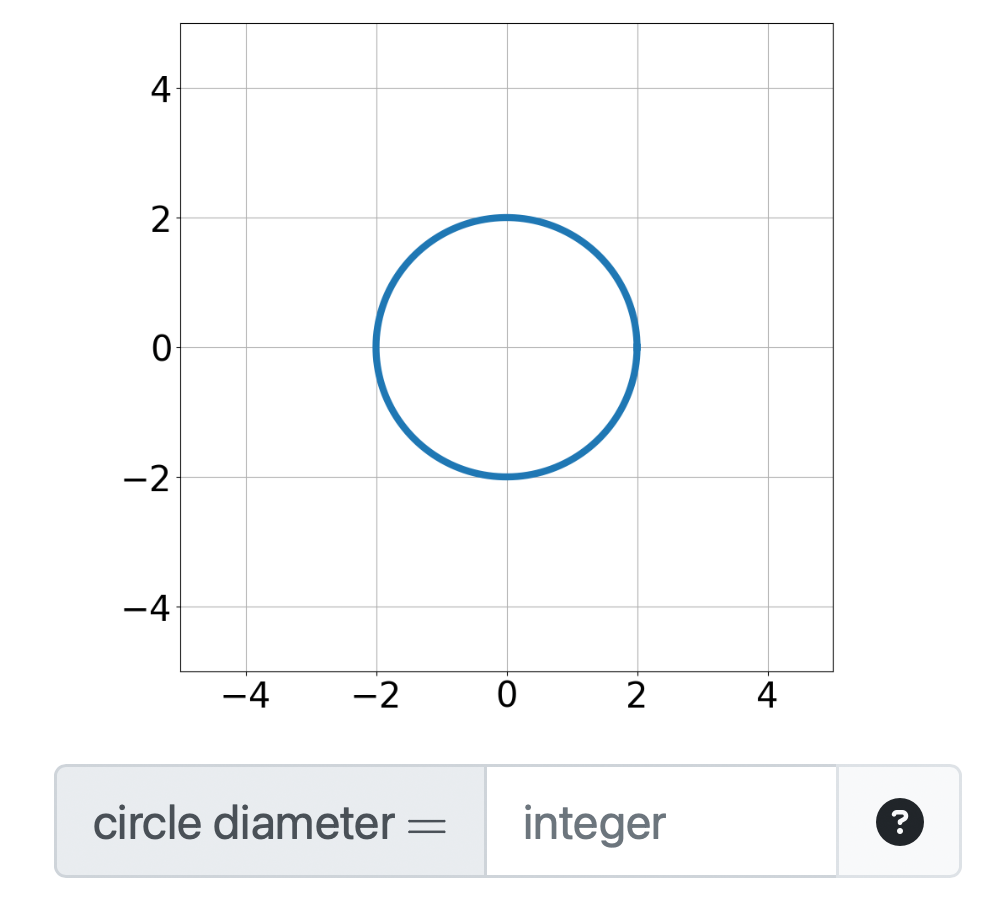
Randomized image
Computes the answer, expected to be an integer, given a dynamically generated image from randomized input parameters.Matrix answers
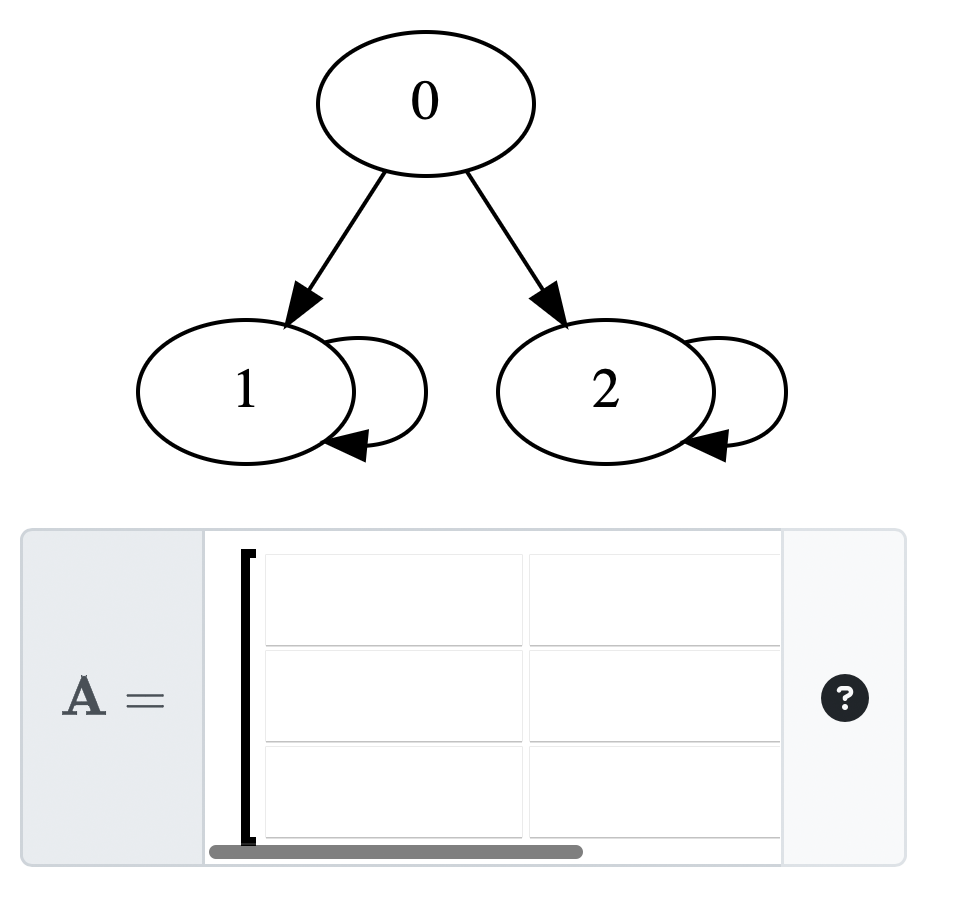
Matrix components
Dynamically generates a randomized graph with nodes and edges, and the answer is the corresponding adjacency matrix.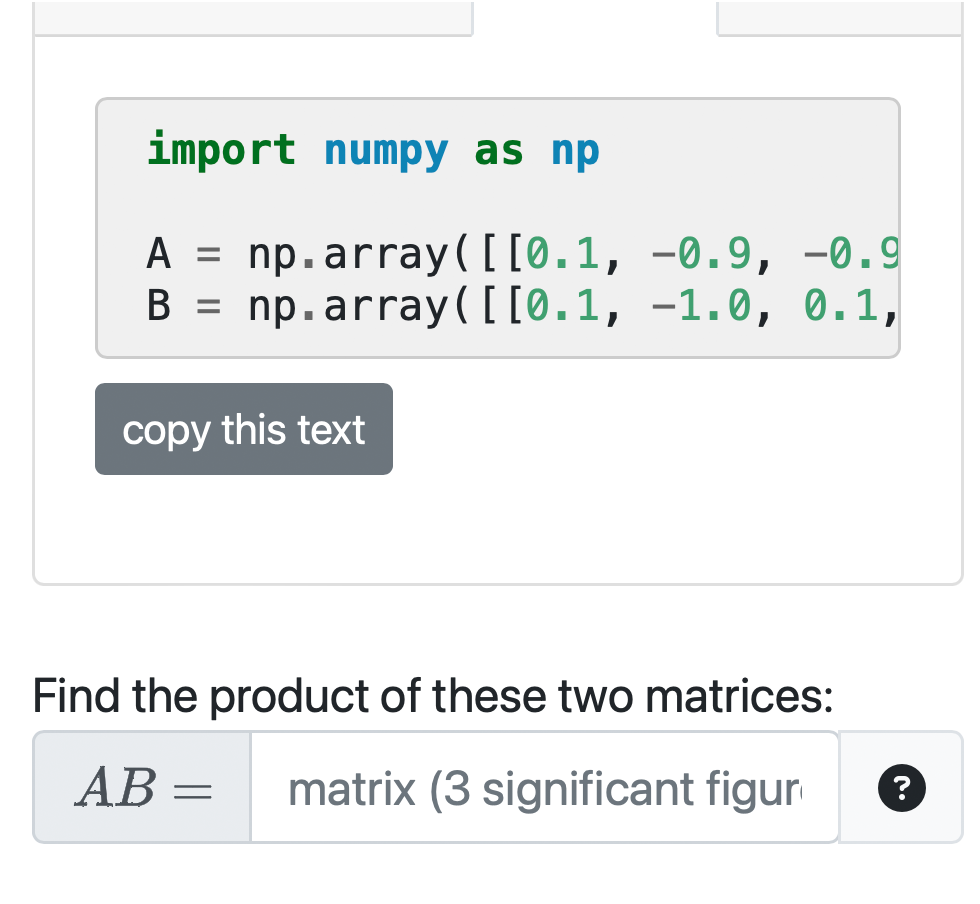
Matrix as code
Generates two randomized matrices and provides them as input in both Matlab and Python format. The computed answer can also be provided in either format.Text answers
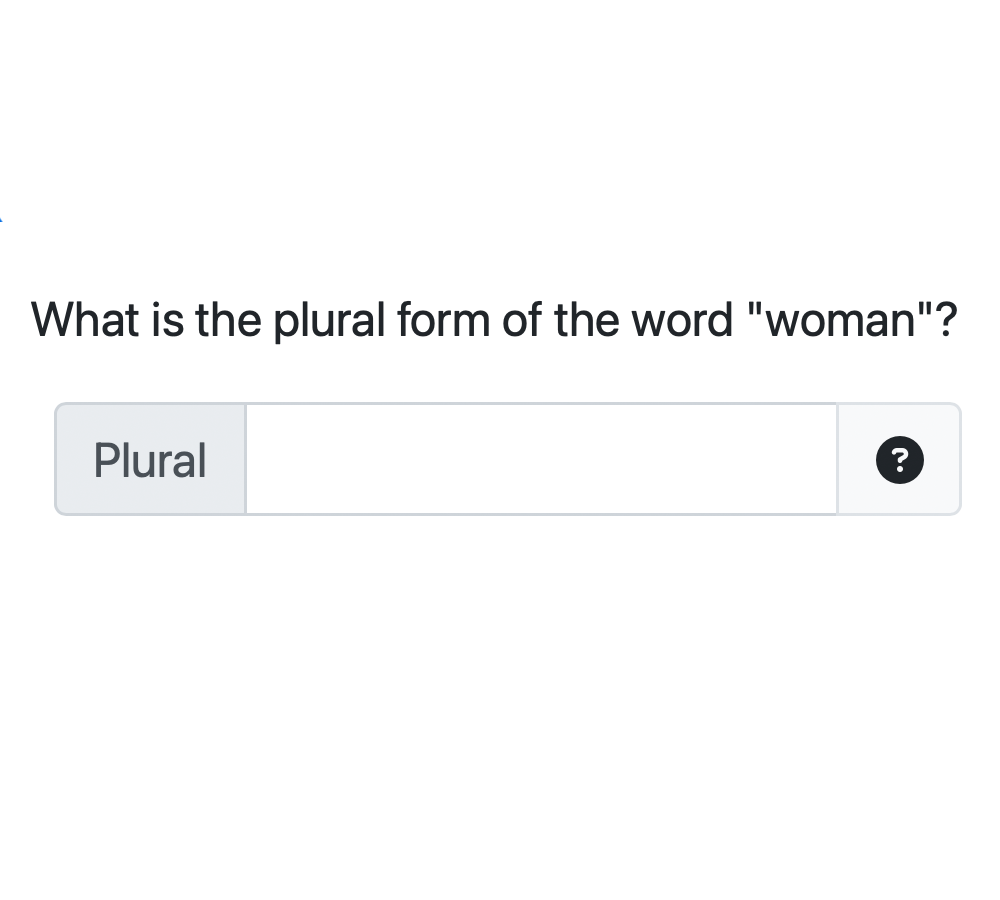
Randomized string
The prompt and correct answer are randomly selected from a list of options. The correct answer is checked as a string, with all whitespace removed.Symbolic expressions

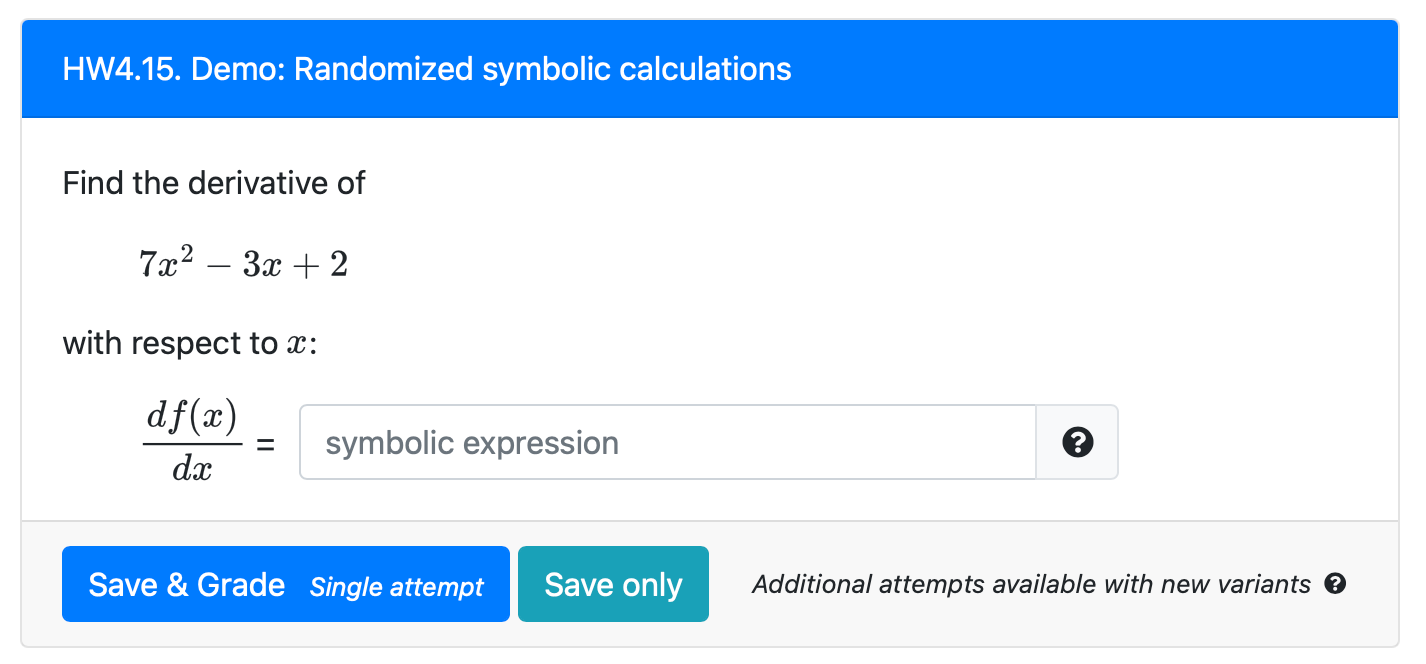
Symbolic answer
Evaluates if a symbolic submission of a mathematical expression matches the correct answer, which is generated at random.View demo course!
Explore the demo course to see how this all comes together